 OK I know, my title doesn’t make any sense. But hear me out:
OK I know, my title doesn’t make any sense. But hear me out:
I’ve told you before about my dear friend Corrine and her amazing château (Latour Segur) near St Emilion. Well, Corrine, whose heart is bigger than my belly (and that is quite a visual I agree), decided to put together a classical concert in her gardens to raise some money. Her goal was to send the 9 kids of our town’s orphanage to Disneyland in Paris.
So, like only she would have the guts to do, Corrine contacted Amira Willighagen’s agent to get her to come down and sing. Amira is a 12 year old opera singer who won Holland’s got talent 2 years ago. Quite the little star in Europe right now!
Corrine also asked our local Aston Martin dealership to participate (which made me even more excited than the opera thing) in the event as well as many local socialites.



The evening was a huge success. She raised the money she needed, and our 9 orphans are off to their promised land.
To be honest, I truly didn’t expect this Amira girl to be any good. I am the kind of guy who switches the channel when I see some kid trying to sing “I will always love you”. Leave my Whitney ALONE!!! It’s just that I believe that one needs to have lived a little before they can bring the kind of emotion such music needs and deserves.

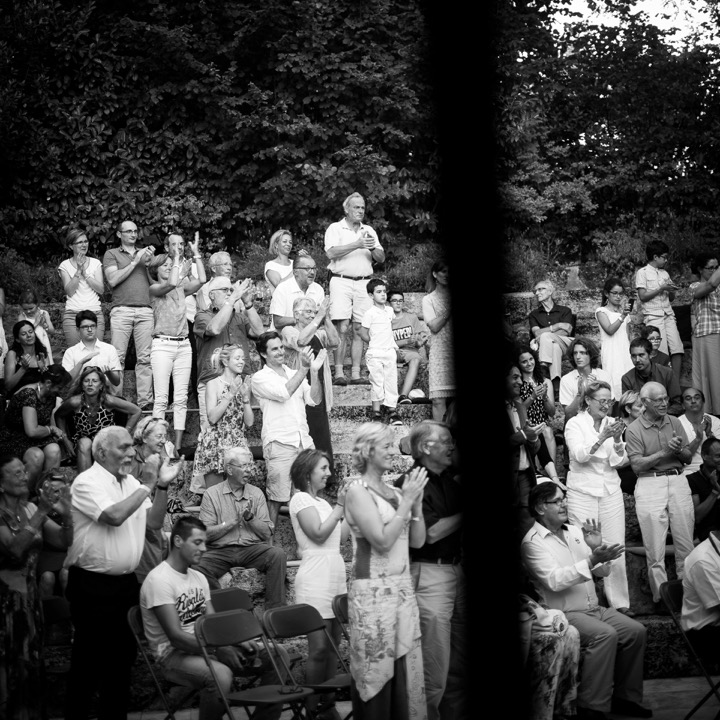


Well, let me tell you. For her age she really delivered! Old soul I guess… Click here for a video of Amira. Then click here for a video of Maria. Because we all deserve to hear a bit of Callas at least once in a while! It’s food for the soul…
Now for the strange title: As I was strolling down through the gardens of the château, I ended up in Corrine’s vegetable garden. The red cabbage looked so stunning in the evening light that I had to take a picture of the damn thing (you know me). I decided that such a nice image shouldn’t go to waste and that I should share it with you. Knowing that you are all greedy little things and would want a recipe to go with it… Here you go:

For 4 people:
- Slice a third of a red cabbage really thin as well as half a carrot and a bit of fresh parsley
- Add vinaigrette to it (1 tablespoon of red wine vinegar for 3 of oil). No mustard this time
- Add one clove of garlic chopped really thin and a fistful of roasted pumpkin seeds (or almonds or walnuts)
- Salt and pepper to taste
- Put the salad in the fridge for about an hour. The vinaigrette will soften the cabbage a bit but it will remain crunchy enough to make your brains go WOW!

I have a red cabbage waiting to be turned into something exciting – looks like I might have found just the recipe!
I hope it made for a great salad Rosie 😉
The cabbage looks delicious and very healthy. I’m growing cabbage for the first time in my garden, so wish me luck!
Alexandra
http://www.theorganizedlist.com
Good choice! They aren’t just delicious, they are very decorative too 😉
Hi Stéphane – I just shared this great post on my foodie facebook page – https://www.facebook.com/cookupastory. Just thought I’d let you know in case?
Thanks my dear! A little help from my friends is always apreciated 😜
Thank you for capturing the event so beautiful that we feel we were there, and then topping it off with a beautiful salad! What more could we want. Stephane delivers again! xo
Why thanks my dear Jodi!!! xoxoxoxo!
This post is awesome all the way around. “leave my Whitney alone…” HA! Beautiful photography, beautiful cabbage and recipe, beautiful voice of Amira. I am so happy the orphans get to go to their promised land!
Don’t you hate it when one of those American Idol idiots butchers your favorite song and gets to be complimented for it? Am I being mean spirited? 😁
No, not at all! My husband feels the same way about Whitney and her songs.
Good man!
I love to read about achievements young people make :). Amira is a treasure! Thanks for introducing her to me. I like the cabbage recipe, too, as I’m eating a lot of the stuff this summer…
Firstly, I LOVE the background of your new blog layout!!! Stunning! Secondly, I’m listening to Amira as I type this – she’s indeed talented. Loved your Whitney comment!!! I would love to meet your friend – she seems like such a tender hearted individual. Fabulous post, as always!
I guess it depends on the format of your screen, but did you notice the angels on the toile de Jouy? My French Heaven? Angels? Get it? I’m so bloody smart 😉 See how our favorite word becomes “bloody” when we’re in public? 😉
you make me laugh my frend!!!
If I can make you laugh and make you eat and make you drink, my job here is done my friend! Oh and “BEAR” with me: it is FRIEND with an “I”. Just sayin(g).
Lovely article.
Amira is gorgeous as well as your pictures! (I even posted about her months ago)…. The event was a wonderful idea! Something someone could replicate in some other corner of the World??
🙂
Have a nice Summer ahead, my dear!
Ps I may try your recipe.
Hello my dear friend! Yes, do try it. I actually thought of you as I was taking the picture of the cabbage in the garden. I remembered some of your stills from a while back… Have a lovely Summer too!!
Corinne has a big heart obviously. A lovely idea for the children.
Did you get to keep the car as a gift bag?
Of course I did Nadia! I was so happy when they told me I could drive it home 😉
As an ardent opera lover since childhood I just hope and pray that this wonderful young girl with that incredibly mature voice has not begun her journey too early . . . that she will have a chance to be a child, a schoolgirl, a silly teenager else her career consumes it all . . .
Beautiful post Stephane! Also would like to say that your website is looking magical these days – stylish, elegant and full of character!
That young voice gave me goose bumps, as you say old soul, and I too hope she continues to sing just because she loves to sing! The purple cabbage in the garden is awesome, not a vegetable but a work of art. Love your simple and delicious salad too!
Thanks my dear. I love red cabbage. Somehow I always think one head is going to make one salad and I end up having enough to eat for a week. When will I learn?!
I always worry when you see such a young person have amazing talent. I hope her family and agents don’t exploit her and cause her downfall like Charlotte Church. To have lasting careers they can’t sprint and ruin the voice. What an amazing trip for those kids though. That is just fabulous.
I had the exact same reaction. For me, these kids were just circus monkeys used by their parents. But I got to see the parents and they are very down to earth people. Simple and humble. The kid seems to really enjoy what she is doing… We will see. I hope she doesn’t fall into the traditional traps…
Fingers crossed!
It’s for posts like this that I follow you. So “You”. Great work.
You’re awsome Conor! You know you are the reason I am blogging again. You gave me the confidence boost I so needed!
A small nudge. You have a wonderful, natural, gift.
How inspiring! And WOW what a voice 🙂
Yes, quite incredible for a girl that age. I hope she doesn’t lose it. She’ll get better as she ages and can put more of herself in what she sings… I wish I’d had such talent at anything when I was her age… Oh, wait, I guess I was really talented at being an absolute brat 😉
What a beautiful story. Wonderful!
Thanks Ashley!
How can a post about a girlish opera singer with huge earrings and a red cabbage make such perfect sense? It does, and your photos are dreamy and a bit mysterious and the story´s like a fairy tale. Wonderful. Sabine.
PS & Back to reality: What´s the huge white blossom in the one photo? In our garden here in PAris, there´s such a thing, reminding me of a magnolia. Do you know its name?
It is indeed magnolia 😉
Magnolia grandiflora Sabine. My favourite form!
Thank you both! I thought so, but the trees have some blossoms here right now, so I thought I was wrong (magnolia bloom is much earlier in Germany)!